- 3. Treće predavanje, Stuttgart, 3 ožujka 1920.
Zastoj povećanja temperature tijekom otapanja i isparavanja. Goetheova fizika. Toplina kao četvrta dimenzija kod Crookesa.
Moji dragi prijatelji,
Da bi danas nastavili prema cilju prvog od ovih predavanja, razmotriti ćemo neke od odnosa između bića topline i takozvanog agregatnog stanja. S ovim agregatnim stanjem mislim na ono na što sam uputio jučer kako je nazvano u drevnom pogledu na fizički svijet, zemlju, vodu, zrak. Upoznati ste s činjenicom da zemlja, voda, i zrak, ili kako se danas zovu, čvrsta, tekuća, i plinovita tijela mogu biti transformirana jedna u drugo. U tom procesu međutim, pokazuje se osobiti fenomen utoliko što se tiče toplinskih odnosa. Najprije ću pokazati pojavu a zatim ćemo je demonstrirati na jednostavan način. Ako odaberemo neko čvrsto tijelo i zagrijavamo ga, postajati će sve toplije i konačno doći do točke kada će iz čvrstog prijeći u tekuće stanje. Pomoću termometra možemo odrediti da kako tijelo apsorbira toplinu, njegova temperatura raste. U trenutku kada se tijelo počinje topiti, postajati tekuće, termometar se prestaje dizati. Ostaje nepokretan sve dok cijelo tijelo ne postane tekućina, i opet se počinje dizati tek kada je sve čvrsto otopljeno. Tako možemo reći: tijekom procesa otapanja, termometar ne pokazuje porast temperature. Međutim iz toga ne treba zaključiti, da ništa topline nije apsorbirano. Jer ako prestanemo grijati, proces otapanja će stati. (Više ću o ovome govoriti poslije.) Toplina mora biti dodavana da bi došlo do otapanja, ali toplina se ne pokazuje u obliku povećanja temperature na termometru. Instrument počinje pokazivati porast temperature tek kada je otapanje potpuno završeno, i tekućina formirana iz čvrstog tijela počinje preuzimati toplinu. Razmotrimo pojavu pažljivo. Jer vidite, ova pojava pokazuje postojanje diskontinuiteta u procesu rasta temperature. Prikupiti ćemo nekolicinu ovakvih činjenica i one nas mogu voditi do sveobuhvatnog pogleda ukoliko ne prijeđemo na neku promišljenu teoriju. Ovdje smo pripremili ovo čvrsto tijelo, natrij tiosulfat (natrijeva sol nap.pr.), kojeg ćemo otopiti. Ovdje vidite temperaturu od oko 25° C. Sada ćemo grijati ovo tijelo i tražim da netko dođe ovamo i gleda temperaturu da potvrdi činjenicu da dok se tijelo otapa temperatura ne raste.(Napomena: Termometar je otišao do 48° C. što je točka otapanja natrij tiosulfata, i ostao tako dok se supstanca nije otopila.) Sada se termometar penje brzo, pošto je otapanje završeno, premda je ostao nepokretan tijekom cijelog procesa otapanja.
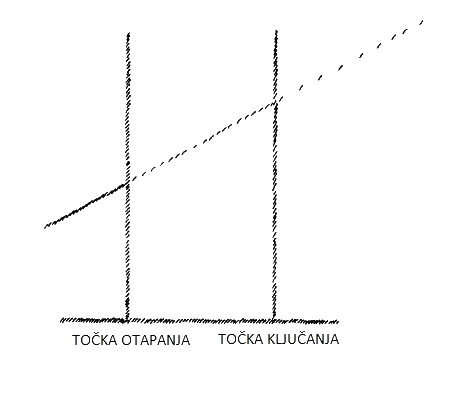
Recimo da ovaj slučaj ilustriramo na jednostavan način, kako slijedi: Porast temperature ćemo smatrati kao liniju nagnutu gore na ovaj način (Slika 1). Recimo da smo podigli temperaturu to točke otapanja, kako je nazvana. Onoliko koliko termometar pokazuje, temperatura opet raste. Može se pokazati da preko ovog daljnjeg porasta temperature, s njegovim odgovarajućim dodatkom topline, tekućina o kojoj se radi se širi. Ako sada grijemo takvo otopljeno tijelo dalje, temperatura ponovno raste od točke na kojoj se odvijalo topljenje (točkasta linija.) Raste dok god tijelo ostaje fluidno. Zatim možemo doći do slijedeće točke na kojoj tekućina počinje ključati. Opet imamo istu pojavu kao i prije. Termometar ne pokazuje daljnji porast temperature sve dok cijela tekućina nije isparila. U trenutku kada je tekućina isparila, držeći termometar u isparenju naći ćemo da opet pokazuje porast temperature (točka-crtica linija.) Možete vidjeti da ovdje tijekom isparavanja instrument ne raste. Tu sam našao drugo mjesto gdje termometar ostaje nepokretan. (Napomena: termometar je ostao na 100° C. u posudi uzavrele vode.)
Sada tražim da činjenici koju sam donio pred vas dodate, drugu koju ćete dobro znati iz uobičajenog iskustva. Ako razmotrite čvrsta tijela, koja čine našu početnu točku, znate da zadržavaju njihov oblik, kakav god oblik da im je dan oni ga održavaju. Ako ovdje pred vas postavim čvrsto tijelo ono ostaje onakvo kakvo je. Ako odaberete tekućinu, odnosno, tijelo koje je primjenom topline prošlo točku otapanja, znate da ga ne mogu nositi komad po komad, već gaje nužno smjestiti u posudu, i ono preuzima oblik posude, formirajući vodoravnu gornju površinu. (Slika 3) Ako odaberem plin — tijelo koje je isparilo prolazeći kroz točku ključanja, ne mogu ga držati u zatvorenoj posudi kakvu koristim za tekućinu, bilo bi izgubljeno. Takav plin ili isparenje mogu držati jedino u posudi zatvorenoj sa svih strana, inače se plin širi vani u svim smjerovima. (Slika 4) To vrijedi, barem za površnu opservaciju, i stvar ćemo razmotriti najprije na ovaj način. A sada bih tražio da napravite slijedeće razmatranje tih stvari sa mnom. Radimo ovo razmatranje da bi spojili činjenice tako da možemo doći do općenite koncepcije o prirodi topline. Sada, da li smo utvrdili porast temperature? Utvrdili smo ga pomoću širenja žive. Širenje se odvijalo u prostoru. I pošto je na našoj uobičajenoj temperaturi živa tekuća, moramo jasno držati na umu da je zatvorena u posudi, i trodimenzionalno širenje je sažeto tako da dobijemo širenje u tom smjeru. Reducirajući širenje žive u tri dimenzije na jednu dimenziju, napravili smo da to širenje mjeri temperaturni porast.
Nastavimo od ove opservacije koju smo postavili kao fundamentalnu i razmotrimo slijedeće: Pretpostavimo liniju (Slika 5) Naravno, linija može postojati jedino u mislima. I pretpostavimo da na ovoj liniji leži nekolicina točaka a, b, c, d, itd. Ako želite dosegnuti ove točke možete ostati u liniji. Ako ste, na primjer, u ovoj točci (a) možete dosegnuti c prolaskom duž linije. Možete ponovno prijeći natrag i opet dosegnuti točku a. Ukratko, ako želim dosegnuti točke a, b, c, d, ja to mogu ostajući potpuno u liniji. Stvar je drugačija ako uzmemo u obzir točku e ili točku f. Ne možete stati u liniji ako želite dosegnuti točku e ili f. Da dosegnete te točke morate izaći vani. Morate ići duž linije a zatim van nje da bi došli do tih točaka.
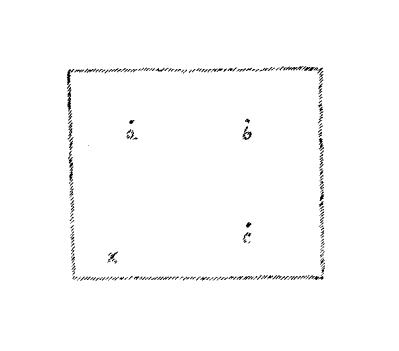
Sada pretpostavite da imate površinu, recimo površinu školske ploče, i ponovno na površini ove ploče lociram nekolicinu točaka; (a,) (b,) (c,) (d.) (Slika 6) Da bi dosegnuli te točke možete uvijek ostati na površini ploče. Ako ste na ovoj točci (x) možete trasirati svoj put do svake od ovih točaka po stazi koja ne napušta školsku ploču. Ne možete, međutim, ako želite ostati na površini ploče, dosegnuti ovu točku koja je na distanci ispred školske ploče. U tom slučaju morate napustiti površinu. Ovo razmatranje vodi do pogleda na dimenzionalnost prostora iz kojeg se može reći: Da bi dosegnuli točke u jednoj dimenziji, dovoljno je kretanje u jednom smjeru, za one u dvije dimenzije pristup im daje kretanje u dvije dimenzije. Nije međutim, moguće dosegnuti točke izvan jedne dimenzije bez napuštanja te dimenzije i slično tome ne može se prijeći kroz točke u tri dimenzije krećući se u samoj ravnini. Što je uključeno kada razmatram točke e i f u odnosu na jednu dimenziju predstavljenu točkama a, b, c, i d? Zamislite biće koje je moglo promatrati samo jednu dimenziju i koje nema pojma o drugoj ili trećoj dimenziji. Takvo biće bi se kretalo u njegovoj jednoj dimenziji baš kao i vi u trodimenzionalnom prostoru. Ako bi takvo biće prenijelo točku a na poziciju b i točka onda skliznula do e, u tom trenutku sadržaj točke bi jednostavno nestao iz jedne dimenzije bića. Od trenutka kada bi napustila jednu dimenziju koje je on svjestan više za ovo biće ne bi postojala. Slično tome točke izvan površine ne bi postojale za biće svjesno samo dvije dimenzije. Kada točka napusti ravninu, takvo biće ne bi imalo načina slijediti je; točka bi nestala iz njegove prostorne oblasti. Kakvu vrstu geometrije bi jednodimenzionalno biće imalo? Imalo bi jednodimenzionalnu geometriju. Moglo bi govoriti samo o udaljenosti i slično, o zakonima povezanim s takvim stvarima kakvi su primijenjeni u jedinoj dimenziji. Dvodimenzionalno biće bi moglo govoriti o zakonima površinskih likova i imalo bi dvodimenzionalnu geometriju. Mi ljudi od početka imamo trodimenzionalnu geometriju. Biće s jednodimenzionalnom geometrijom ne bi imalo mogućnost razumijevanja što točka čini kada napušta jedinu dimenziju. Biće s dvodimenzionalnom geometrijom ne bi moglo slijediti kretanje točke koja napušta površinu i izlazi ispred nje kao što smo pretpostavili da je bio slučaj kada točka napušta površinu i izlazi vani ispred nje kao što smo pretpostavili da je slučaj kada točka napušta površinu školske ploče. Mi ljudi — ponovno navodim — imamo trodimenzionalnu geometriju. Sada bi upravo mogao učiniti ono što sam obvezan učiniti na račun reduciranja trodimenzionalnog širenja žive na jednu dimenziju. Mogu nacrtati dvije linije u dva smjera tako da čine sustav osi, tako dajući kao na Slici 7 os apscise i os ordinate. Pod pravim kutovima na ravnine to dvoje, pretpostavimo da imamo treću liniju koju ćemo nazvati prostorna linija. (Pozivajući se ponovno na dijagram temperaturnog rasta – pr). Čim dođem ili do točke taljenja ili do točke ključanja, u tom trenutku nisam u poziciji da nastavim s linijom (Slika 8). Teoretski ili hipotetski nema mogućnosti za nastavljanje linije. Pretpostavimo da možemo reći, porast temperature je predstavljen ovom linijom. Možemo nastaviti duž nje i još uvijek imamo točku povezanosti s našim uobičajenim svijetom. Ali mi u stvari nemamo takvu točku povezanosti. Jer kada crtam ovu temperaturnu krivulju i dođem do točke otapanja ili ključanja, mogu samo krivulju nastaviti od iste točke (x, x na Slici 8). Koju sam dosegnuo kada se tijelo počelo otapati ili isparavati. Iz toga vidite, da s obzirom na točku otapanja ili isparavanja, ja sam u poziciji koja se ne razlikuje od one od jednodimenzionalnog bića kada se točka kreće izvan njegove prve dimenzije u drugu dimenziju, ili dvodimenzionalnog bića kada za njega točka nestaje u trećoj dimenziji. Kada se točka ponovno vraća i počinje od istog mjesta, ili kao na Slici 5 kada točka ide vani na jednu stranu i vraća se, tada je nužno nastaviti liniju u njegovoj jednoj dimenziji. Smatrano jednostavno za promotrenu pojavu, kada temperaturni porast nestaje na točci otapanja i ključanja, to je kao da mi je temperaturna krivulja slomljena, i nakon nekog vremena moram nastaviti od iste točke. Ali što se događa s toplinom dok ovaj prekid pada izvan oblasti u kojoj crtam moju krivulju. Formalno govoreći, mogu reći da to mogu nacrtati na prostornoj liniji. Postoji, na prvi pogled — primijetite da kažem na prvi pogled — analogija prisutna između nestanka točke a iz prve a u drugu dimenziju i onog što se događa temperaturi koju pokazuje termometar kada instrument miruje na točci otapanja i točci isparavanja.
Sada još jednu pojavu moramo dovesti u vezu s ovim. Molim da primijetite da ovim povezivanjem pojava mi napredujemo, ne u elaboriranju neke vrste teorije, već dovodeći pojave zajedno tako da prirodno osvijetle jedna drugu. Tu je distinkcija između fizike Goethea koja jednostavno smješta pojave jednu do druge tako da bacaju svijetlo jedna na drugu, i moderne fizike koja teži prijeći u teorije, i da promišljene elaboracije doda činjenicama. Jer atomi i molekule nisu ništa drugo nego fantazije dodane činjenicama.
Razmotrimo sada još jednu pojavu pored ovog nestanka temperature zabilježenog od termometra tijekom procesa otapanja. S tom drugom pojavom se susrećemo kada pogledamo jučerašnju formulu. Bila je napisana ova formula:
V - Vo (1 + 3αt + 3α2t2 + α3t3)
Sjećate se da sam jučer rekao da posebnu pažnju trebate obratiti na zadnja dva izraza. Posebno nam je važno u isto vrijeme uzeti u obzir t3, treću potenciju temperature. Zamislite na trenutak uobičajeni prostor. U tom običnom prostoru u matematičkim izrazima govorite o dužini, širini, i debljini. One su u stvari tri dimenzije prostora. Sada kada zagrijavamo štap, kao što smo napravili jučer, možemo promatrati širenje tog štapa. Možemo također primijetiti temperaturu tog štapa. Postoji jedna stvar koju ne možemo urediti. Ne možemo srediti to da štap dok se širi, ne ispušta toplinu u svoje okruženje, to da ne struji ili zrači toplinu. To ne možemo spriječiti. Nemoguće je za nas misliti — primijetite riječ — o propagaciji topline u jednoj dimenziji. Možemo zaista misliti o prostornoj ekstenziji u jednoj dimenziji kao što se radi u geometriji u slučaju linije. Ali pod bilo kakvim okolnostima ne možemo zamisliti toplinu propagiranu duž linije. Kada to razmatramo ne možemo reći da se o propagaciji topline može promišljati kao da je stvarno predstavljena u prostoru linijom koju sam nacrtao ovdje. (Slika 1) Ta krivulja za mene ne predstavlja cijeli proces uključen u zagrijavanje. Aktivno je još nešto osim toga što mogu zaključiti iz krivulje. I aktivnost tog nečeg mijenja cijelu prirodu i biće onog što je prikazano tom krivuljom, koju koristim kao simbol koji se jednako može smatrati kao čisto aritmetička ili geometrijska činjenica.
Imamo, dakle, čudnu situaciju. Kada pokušamo shvatiti toplinsko stanje, utoliko što to stanje pokazuje temperatura, pomoću obične geometrijske linije, nalazimo da se to ne može. Sada to ima još jedan smjer. Zamislite na trenutak da imam liniju. Ta linija ima određenu dužinu: l (Slika 9) Kvadriram tu liniju, i tada to l2 mogu predstaviti kvadratnom površinom. Recimo da dobijem l3 tada mogu treću potenciju predstaviti kockom, čvrstim tijelom. Ali recimo da dobijem četvrtu potenciju, l4. Kako to mogu predstaviti? Mogu prijeći od linije na površinu, od površine na čvrsto tijelo, ali što mogu napraviti slijedeći istu metodu ako želim predstaviti četvrtu potenciju? Ne mogu napraviti ništa ako ostanem u našem trodimenzionalnom prostoru. Matematičko razmatranje to pokazuje. Ali vidjeli smo da se toplinsko stanje utoliko što je otkriveno temperaturom ne može izraziti prostornim terminima. Postoji još nešto u njemu. Ako ne bi bilo, mogli bi zamišljati stanje topline kako prolazi duž štapa potpuno ograničeno na štap. To je, međutim, nemoguće. Posljedica ovoga je da ako zaista želim raditi u ovoj oblasti, ne bih trebalo gledati na potencije od ‘t’ na isti način kao potencije kvantiteta mjerenog u prostoru. Ne mogu misliti o potencijama od ‘t’ na isti način kao onima od ‘l’ ili bilo kojeg drugog samo prostornog kvantiteta. Kada, na primjer, i to ću sutra razmatrati hipotetski, kada imam prvu potenciju i nađem da se ne može izraziti linijom, tada ni druga potencija t2 ne može biti izražena kao površina i zasigurno treća potencija t3 ne može biti izražena kao čvrsto tijelo. U čisto matematičkom prostoru, tek nakon što sam dobio treću potenciju izlazim iz običnog prostora, ali u ovom drugom slučaju ja sam sasvim izvan običnog prostora u slučaju druge potencije a i treće isto tako.
Stoga, morate shvatiti da t morate pojmiti kao sasvim različito u njenoj prirodi od prostornih kvantiteta. Morate smatrati t kao nešto već kvadrirano, kao drugu potenciju a o kvadriranom t morate misliti kao o trećoj potenciji, o t na kub kao o četvrtoj potenciji. To nas vodi izvan običnog prostora. Razmotrite sada kako ovo daje našoj formuli veoma poseban aspekt. Jer zadnji član, koji je u ovom super-prostoru, sili me da izađem iz običnog prostora. U takvom slučaju kada se ograničim na računanje moram ići izvan trodimenzionalnog prostora za zadnji član formule. Imam takvu mogućnost u čisto matematičkoj formuli.
Kada promatrate trokut i odredite da ima tri kuta, bavite se, za početak, s zamišljenim trokutom. Pošto samo mišljenje o njemu nije dovoljno da zadovolji vaša čula, vi ga crtate, ali crtanje ne dodaje ništa vašoj ideji. Dobili ste, zbroj kutova je 180, ili pravokutni trokut — kvadrat hipotenuze jednak je zbroju kvadrata ostale dvije strane. Ove stvari su obrađene kao što ja sada obrađujem potenciju od ‘t.’
Sada se vratimo i vidimo što smo utemeljili kao činjenicu. Ovako je to napravljeno u geometriji. Uvijek je točno da kada promatram stvarni trokut u konstrukciji mosta ili drugdje, apstraktna ideja se potvrđuje. Ono što sam razmišljao o apstraktnom ‘t‘ ima na početku sličnosti s topljenjem i isparavanjem. (Postepeno ćemo se približiti esenciji stvarnosti.) Otapanje i isparavanje ne mogu izraziti pomoću tri dimenzije prostora. Jedini način na koji ih mogu natjerati u krivulju bio je da stanem i onda opet nastavim. Da bih dokazao hipotezu koju sam vam napravio, bilo je nužno, u slučaju treće potencije, kuba temperature, ići izvan trodimenzionalnog prostora.
Vidite, pokazujem vam kako moramo, takoreći, razbiti stazu ako želimo zajedno smjestiti one pojave koje jednostavno time što su stavljene jedna do druge ilustriraju biće topline i omogućavaju nam da steknemo razumijevanje slično onom do kojeg smo došli u prethodnom ciklusu o svjetlosti.
Fizičar Crookes je pristupio ovoj temi s potpuno drugačijom hipotezom. Značajno je da su ga njegova razmatranja dovela do rezultata sličnog onom do kojeg smo i mi stigli privremeno i čiju valjanost ćemo utemeljiti na slijedećim predavanjima. Također je zaključio da je promjena temperature u biti imala veze s vrstom četvrte dimenzije u prostoru. U ovo vrijeme je važno dati pažnju ovim stvarima jer se relativisti, s Einsteinom na čelu, osjećaju obvezni kada idu izvan trodimenzionalnog prostora, smatrati vrijeme kao četvrtu dimenziju. Tako, u Einsteinovim formulama, svuda se može naći vrijeme kao četvrta dimenzija. Crookes je, s druge strane, smatrao stjecanje ili gubitak topline za četvrtu dimenziju. Toliko o ovim usputnim podacima o povijesnom razvoju.
Tražio bih da ovim pojavama sada dodate ono što sam prije naglasio. Rekao sam: Običnim čvrstim tijelom može se rukovati i ono će zadržati njegov oblik, (Slika 2). Odnosno, ima determiniranu granicu. Tekućinu treba uliti u posudu, (Slika 3). Ona uvijek formira ravnu gornju površinu a ostatak poprima oblik posude. Nije tako kod plina ili kod parnog tijela koje se širi u svim smjerovima. Da bi ga zadržao, moram ga smjestiti u posudu zatvorenu sa svih strana, (Slika 4). Ta potpuno zatvorena posuda daje mu svoju formu. Dakle, u slučaju plina, imam formu tek kada ga zatvorim u posudu zatvorenu sa svih strana. Čvrsto tijelo posjeduje formu jednostavno pomoću činjenice da je čvrsto tijelo. Ono ima formu samo po sebi, takoreći. Smatrajući tekuće za srednje stanje, primijetiti ćemo da se čvrsta i plinovita tijela mogu opisati kao suprotnosti. Čvrsta tijela snabdijevaju sebe s onim što moram dodati plinovitom tijelu, naime potpuno okružujuću granicu.
Sada se, međutim, čudna stvar javlja kod plina. Kada stavljate plin u manji volumen (Slika 10), koristeći istu količinu plina ali skupljanjem svih okolnih zidova, morate koristiti pritisak. Morate izvršiti pritisak. To ne znači ništa drugo nego da morate nadvladati pritisak plina. To radite vršeći pritisak na zidove koji daju oblik plinu. Stvar možemo izjaviti ovako: da je plin koji ima tendenciju da se širi u svim smjerovima držan na okupu otporom graničnih zidova. Taj otpor je u slučaju čvrstih tijela tamo sam po sebi. Tako da, bez ikakvog teoretiziranja, već jednostavno imajući na umu sasvim očigledne činjenice, polarni kontrast između plina i čvrstog tijela mogu definirati na slijedeći način: Ono što plinu moram dodati od izvana u čvrstom tijelu je prisutno samo po sebi. Ali sada, ako hladite plin, možete ponovno priječi natrag do točke ključanja i od isparenja dobiti tekućinu, i ako hladite dalje do točke otapanja, iz tekućeg možete dobiti čvrsto tijelo. Odnosno, možete procesima povezanim s toplinskim stanjem dovesti do takvog stanja da formu više ne morate graditi izvana, već se stvaranje forme odvija samo po sebi od iznutra. Pošto nisam napravio ništa već doveo do promjene toplinskog stanja, samo je po sebi razumljivo da je forma na neki način povezana s promjenama u toplinskom stanju. U čvrstom tijelu, prisutno je nešto što nije prisutno u plinu. Ako nasuprot čvrstom tijelu držimo zid, čvrsto tijelo samo po sebi ne vrši pritisak na zid ukoliko mi samo ne dovedemo do toga. Kada, međutim, zatvorimo plin u posudu, plin pritiska čvrste zidove. Vidite, dolazimo do koncepta pritiska i to stvaranje pritiska moramo dovesti u vezu s toplinskim stanjem. Moramo sebi reći: nužno je naći egzaktnu relaciju između oblika čvrstih tijela, tendencije difuziji plinova i suprotstavljanju graničnih zidova koji se suprotstavljaju toj difuziji. Kada znamo tu relaciju možemo se nadati da ćemo stvarno ići naprijed u relaciju između topline i tjelesnosti.
Slika 1

Slika 2

Slika 3

Slika 4

Slika 5
Slika 6
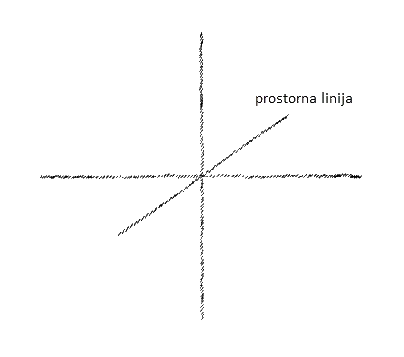
Slika 7

Slika 8

Slika 9

Slika 10
 .
.