- 9. Deveto predavanje, Stuttgart, 9. siječnja 1921.
Elipsa, hiperbola, Cassinijeva krivulja, krug kao krivulje zbroja, razlike, umnoška, kvocijenta. 4 oblika krivulje Cassini. Beskonačno udaljena točka pravca.
Moji dragi prijatelji,
Sada smo u našim proučavanjima došli do točke od koje moramo nastaviti s ekstremnim oprezom, da bi vidjeli gdje postoji opasnost da naša misao odstupi od stvarnosti i također da vidimo kada tu opasnost izbjegavamo, držeći se unutar granica onog što je stvarno.
Zadnji puta, predložili smo usporedbu dvije činjenice: pojavu kometa unutar planetarnog sustava, i, na kraju krajeva opet unutar planetarnog sustava, premda možda ne nosi sasvim jednak odnos prema njemu, sve što promatramo kod pojave oplodnje. Međutim, da bi došli do ideja o ovome što smo upravo obrazložili, najprije moramo vidjeti da li je zaista moguće pronaći vezu između dvije toliko razdvojene stvari, s kojima smo suočeni u vanjskom svijetu činjenica. Metodološki nećemo doći ni do kakvog cilja, ukoliko ne možemo ukazati na bilo što, gdje se radi o nečem sličnom, a što bi nas potom moglo voditi dalje u načinu gledanja na stvari.
Vidjeli smo kako u jednu ruku moramo koristiti element oblika, forme, matematički, i zatim kako smo stalno prinuđeni na ovaj ili onaj način primijeniti kvalitativni aspekt, na neki način pristupiti kvalitativno. I tako ćemo danas uvesti nešto što se pojavljuje u odnosu na čovjeka ako se tog čovjeka zaista proučava, a koji je, konačno, na neki način slika nebeskih pojava, — kao što nam mnoge izjave na ovim predavanjima omogućuju da zaključimo. Ipak još uvijek moramo ustanoviti na koji je način on ta slika. Ako je to ono što on jest, moramo prije svega steći jasno razumijevanje samog čovjeka. Moramo shvatiti sliku od koje namjeravamo krenuti, — shvatiti njenu unutarnju perspektivu. Baš kao što se pri gledanju na sliku treba znati što skraćena perspektiva znači, i tako dalje, da bi od slike prešli na stvarne prostorne odnose i sliku povezali s onim što predstavlja u stvarnosti, dakle, ako ćemo u univerzumu pristupiti stvarnosti, interpretirajući je kroz čovjeka, najprije nam mora biti jasan čovjek. Sada, iznimno je teško, kao ljudskom biću, približiti se ljudskom biću s opipljivim idejama. Stoga, danas bih pred vaše duše želio postaviti ono što bih mogao nazvati „opipljive-neopipljive“ misaone slike koje dolaze iz sasvim jednostavnih osnova, ideja s kojima ste mnogi od vas vjerojatno dobro upoznati, ali koje ipak moramo postaviti pred naše umove u određenom kontekstu. Te ideje, koje izgledaju kao da ih je djelomično sasvim lako dokučiti a ipak, van izvjesnih granica, izmiču našem razumijevanju, priuštiti će nam orijentaciju u težnji da vanjski svijet zahvatimo kroz ideje.
Može izgledati nekako isforsirano stalno naglašavati nužnost upućivanja natrag na čovjekov život slikovne imaginacije da bi razumjeli pojave nebesa. Ali konačno, očigledno je da koliko god pažljivo opisivali nebeske pojave, za početak, nemamo ništa više od vrste optičke slike, prožete matematičkim mislima. Ono što nam astronomija daje u osnovi ima karakter slike. Da bi bili na pravom putu, moramo se stoga pozabaviti s pojavom slike u čovjeku, inače nećemo doći do pravog odnosa prema onom što nam astronomija može reći. I tako bih danas želio krenuti od sasvim jednostavne matematike i pokazati vam kako se, u različitoj domeni od one u koju smo vođeni preko omjera perioda revolucije planeta, tamo unutar same matematike pojavljuje taj element neshvatljivog, neopipljivog. S njime se susrećemo kada u određenoj vezi proučavamo sasvim poznate krivulje. (Kao što sam rekao, mnogi od vas već znaju ono što ću opisati, danas samo želim temu rasvijetliti s određenog aspekta.)
Razmotrite elipsu, s njena dva žarišta A i B, i znate da je definicija elipse da za bilo koju točku M na krivulji, suma njenih udaljenosti (a + b) od dva žarišta ostaje konstantna. To je osobina elipse, da suma udaljenosti bilo koje njene točke od dvije fiksne točke, dva fokusa, ostaje konstantna (Slika 1).

Slika 1

Slika 2
Zatim imamo drugu krivulju, hiperbolu (Slika 2). Znate da ona ima dva ogranka. Ona je definirana u tome što je razlika udaljenosti bilo koje točke krivulje od dva žarišta, (b - a) konstantna veličina. Kod elipse, dakle, imamo krivulju konstantne sume, kod hiperbole, krivulju konstantne razlike, i sada moramo pitati: koja je to krivulja konstantnog umnoška?

Slika 3
Često sam skretao pažnju na ovo: krivulja konstantnog umnoška je takozvana krivulja Cassini (Slika 3). Nalazimo je kada, imajući dvije točke, A i B, računamo točku M s obzirom na njene udaljenosti od A i B, i uspostavimo uvjet da dvije udaljenosti AM i BM pomnožene zajedno moraju biti konstantne veličine. Zbog jednostavnosti proračuna, konstantnu veličinu ću zvati b2 a udaljenost AB, 2a. Ako središnju točku između A i B uzmemo kao središte osi koordinatnog sustava i računamo ordinate za svaku točku koja ispunjava te uvjete, — uzmite C kao središte koordinatnog sustava i neka se točka čiju ordinatu ćemo nazvati y kreće okolo tako da za svaku točku krivulje AM x BM = b2 , dobijemo slijedeću jednadžbu. (Dati ću vam samo rezultat, iz jednostavnog razloga jer svatko može izračun napraviti za sebe; naći će se u svakom matematičkom priručniku u vezi teme.) Za y nalazimo vrijednost:
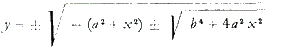
Uzimajući ovdje u obzir da ne možemo koristiti negativan predznak jer bi tada trebali imati imaginarno y, i stoga uzimajući u obzir samo pozitivan predznak, imamo:
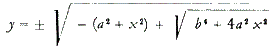
Ako zatim crtamo odgovarajuću krivulju, dobijemo krivulju, sličnu ali ne identičnu elipsi, nazvanu krivulja Cassini (Slika 4). Simetrična je s lijeve i desne strane osi ordinate te povrh i ispod osi apscise.

Slika 4
Ali sada, ova krivulja ima razne forme, i za nas je to u svakom slučaju važna stvar. Krivulja ima različite forme, prema tome da li je b, kako sam ga ovdje uzeo, veće od a, jednako a, ili manje od a. Krivulja koju sam upravo nacrtao javlja se kada je b > a, i osim toga kada je ispunjen još jedan uvjet, naime, da je b također veće ili jednako a√2. Štoviše, kada je b > a√2, postoji posebna zakrivljenost iznad i ispod, ako je b = a√2, tada u toj točci iznad i ispod, linija krivulje postaje ispravljena, izravnava se toliko da gotovo postaje ravna linija (Slika 4). Ako je, međutim, b < a√2, tada je cijeli tijek linije promijenjen i uzima ovaj oblik (Slika 5). A ako je b = a, krivulja prelazi u sasvim poseban oblik, mijenja se u ovaj oblik (Slika 6). Ide natrag u sebe, presijeca sebe i izlazi na drugoj strani, i dobijemo poseban oblik lemniskate. Lemniskata je, dakle, poseban oblik krivulje Cassini — te krivulje su tako nazvane po njihovim pronalazačima. Konkretan oblik koji krivulje poprimaju određen je omjerom između konstantnih veličina koje se pojavljuju u jednadžbi koja opisuje krivulju. U jednadžbi, imamo samo ove dvije konstantne veličine, b i a, i oblik krivulje zavisi o omjeru između njih.

Slika 5
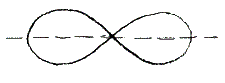
Slika 6
Zatim je moguć treći slučaj, da je b < a. Ako je b < a, još uvijek možemo naći vrijednosti za krivulju. Možemo uvijek riješiti jednadžbu i dobiti vrijednosti za krivulju, ordinatu i apscisu, čak i kada je b manje od a, jedino što tada krivulja prolazi kroz još jednu metamorfozu. Jer kada je b < a, nalazimo dva ogranka krivulje, koji izgledaju nekako ovako (Slika 7). Imamo diskontinuiranu krivulju. I ovdje dolazimo do točke gdje nas sama matematika suočava s onim što sam nazvao „shvatljivo-neshvatljivo“, nečim što je teško shvatiti u prostoru. Jer u smislu matematičke jednadžbe, to nisu dvije krivulje, već jedna; to je jedna krivulja upravo na isti način kao što su sve ove pojedinačne krivulje (Slike 3 do 5). Kod ove (lemniskata) već postoji tranzicija. Točka koja opisuje krivulju ide ovako, ide okolo odozdo, siječe svoju prethodnu stazu i nastavlja ovdje (Slika 7). Ovdje, moramo predstaviti sljedeće: Ako pustimo da se točka M kreće po ovoj liniji, ona ne prelazi jednostavno s jedne strane na drugu, — to ne radi. Ona ide duž putanje kao i kod ostalih krivulja, opisuje ovdje krivulju, ali zatim se ovdje uspijeva opet pojaviti. (Slika 7) Vidite, ono što nosi točku duž linije nestaje ovdje u sredini. Ako krivulju želite razumjeti možete samo zamisliti da nestaje u sredini. Ako pokušate oblikovati kontinuiranu mentalnu sliku ove krivulje, što morate napraviti?

Slika 7
Sasvim je lako, zar ne, zamisliti ovakve krivulje. (Ovo umećem samo za sitničave!) Možete nastaviti zamišljati točke duž krivulje i ne nalazite da se slika prekida. Ovdje (kod lemniskate) doduše, morate promijeniti ugodan način da jednostavno idete u krug, ali još uvijek ide kontinuirano. Još se možete držati mentalne slike. Ali sada, kada dođete do ove krivulje (Slika 7), koja nije tako banalna, i želite je zamisliti, tada ćete, da bi zadržali kontinuitet ideje morati reći: prostor mi više ne pruža točku potpore. Pri prelasku na drugi ogranak u mojoj imaginaciji, ukoliko ne prekidam kontinuitet i jedan ogranak ne gledam kao nezavisan od drugog, moram izaći iz prostora; ne mogu jednostavno ostati u prostoru. Dakle vidite, sama matematika nam daje činjenice koje nas obvezuju da idemo izvan prostora, ako ćemo sačuvati kontinuitet ideje. Sama stvarnost od nas zahtijeva da u našim idejama idemo izvan prostora. Stoga smo čak i u matematici suočeni s nečim što nam pokazuje da na neki način prostor moramo ostaviti iza, ako će čista ideja slijediti svoj pravi put. Ono što smo napravili prateći ideju početak je promišljanja procesa, moramo nastaviti razmišljati na takav način da nam prostor više nije ni od kakve pomoći. Ako to ne bi bilo tako, ne bismo trebali moći izračunati sve mogućnosti u jednadžbi.
Prateći sličnu liniju misli, susrećemo se s drugim primjerima ovakve vrste. Skrenuti ću vašu pažnju samo na sljedeći korak, koji odgovara ako se razmišlja kako slijedi. Elipsa je geometrijsko mjesto konstantne sume, — definirana je činjenicom da je krivulja konstantne sume. Hiperbola je krivulja konstantne razlike. Krivulja Cassini u njenim raznim oblicima je krivulja konstantnog umnoška. Morala bi dakle postojati i krivulja konstantnog kvocijenta također, ako ovdje imamo A, ovdje B, ovdje točku M, i zatim konstantni kvocijent bude formiran kroz dijeljenje BM sa AM. Morali bi moći naći različite točke, M 1, M 2, itd., za koje je
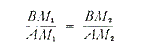
itd. jednako jedno drugom i uvijek jednako konstantnom broju. Ova krivulja je, u stvari, kružnica. Ako potražimo točke M1, M2 itd. nalazimo kružnicu koja ima ovaj konkretan odnos s točkama A i B (Slika 8). Tako da možemo reći: osim uobičajene, jednostavne definicije kružnice, — naime, da je to geometrijsko mjesto točaka čije udaljenosti od fiksne točke ostaju konstantne, — postoji još jedna definicija. Kružnica je takva krivulja, čija svaka točka ispunjava uvjet da njihove udaljenosti od dvije fiksne točke zadržavaju konstantni kvocijent.

Slika 8
Sada, razmatrajući krug na ovaj način još nešto se može vidjeti. Jer vidite, ako izrazimo ovo
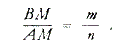
(to se naravno može izraziti na neki drugi način), uvijek dobijemo odgovarajuće vrijednosti u jednadžbi, i možemo naći kružnicu. Radeći to nalazimo različite oblike kružnice (odnosno, različite proporcije između radijusa kružnice i duljine ravne linije AB), u skladu sa omjerom m prema n. Ti različiti oblici kružnice ponašaju se na takav način da njihova zakrivljenost postaje sve manja i manja. Kada je n mnogo veće od m, imamo kružnicu s veoma jakom zakrivljenošću; kada n nije toliko mnogo veći, zakrivljenost je manja. Kružnica postaje sve veća što je manja razlika između n i m. I ako taj omjer m prema n pratimo dalje, kružnica postupno prelazi u ravnu liniju. To možete slijediti u jednadžbi. Prelazi u samu os ordinate. Kružnica postaje os ordinate kada je m = n, odnosno, kada je kvocijent m/n = 1. Na ovaj način kružnica se postupno mijenja u os ordinate, u ravnu liniju.
Kod ovoga ne trebate biti posebno začuđeni. To je sasvim moguće zamisliti. Međutim nešto se sasvim drugačije događa ako proces želimo slijediti još i dalje. Kružnica je sve više izravnata, i postajući izravnata od iznutra, takoreći, mijenja se u ravnu liniju. To radi jer konstantni omjer u jednadžbi pretrpljuje promjenu. Kroz to kružnica postaje ravna linija. Ali ovaj konstantni omjer može naravno rasti izvan 1, tako da se lukovi kružnica pojavljuju ovdje (na lijevo od osi y). Međutim, što moramo napraviti, ako je pokušamo slijediti u našoj imaginaciji? Moramo napraviti nešto sasvim osobito. Moramo, u stvari, misliti o kružnici koja nije zakrivljena prema unutra, već je zakrivljena prema vani. Naravno, ne mogu nacrtati tu kružnicu, ali moguće je misliti o kružnici koja je zakrivljena prema vani.[ako bi je nacrtali izgledala bi kao obična kružnica, jedino bi trebalo imati na umu da su „vani“ i „unutra“ zamijenili mjesta] Kod obične kružnice zakrivljenost je prema unutra, zar ne? Ako liniju pratimo okolo ona se vraća u sebe. Ali definirajući kružnicu na ovaj drugi način, ako koristimo nužnu konstantu, dobijemo ravnu liniju. Zakrivljenost je još na ovoj strani (desno od osi y). Ali sada stvari čini ni blizu tako ugodnima kao ranije! Ranije, zakrivljenost je uvijek okrenuta prema središtu kružnice, dok nam je sada (u slučaju ravne linije), pokazano da je središte negdje na beskonačnoj udaljenosti, kako se kaže. Idući dalje od ovoga, za nas je javlja ideja o kružnici koja je zakrivljena prema vani. Njena zakrivljenost nije više kao ovdje (Slika 9a) — to bi bila obična, otrcana, filistarska kružnica, — već je njena zakrivljenost ovdje (Slika 9b). Dakle, unutrašnjost ove kružnice nije ovdje; ovo je izvana; unutrašnjost ove kružnice (Slika 9c) je na desno.
Kod ovoga ne trebate biti posebno začuđeni. To je sasvim moguće zamisliti. Međutim nešto se sasvim drugačije događa ako proces želimo slijediti još i dalje. Kružnica je sve više izravnata, i postajući izravnata od iznutra, takoreći, mijenja se u ravnu liniju. To radi jer konstantni omjer u jednadžbi pretrpljuje promjenu. Kroz to kružnica postaje ravna linija. Ali ovaj konstantni omjer može naravno rasti izvan 1, tako da se lukovi kružnica pojavljuju ovdje (na lijevo od osi y). Međutim, što moramo napraviti, ako je pokušamo slijediti u našoj imaginaciji? Moramo napraviti nešto sasvim osobito. Moramo, u stvari, misliti o kružnici koja nije zakrivljena prema unutra, već je zakrivljena prema vani. Naravno, ne mogu nacrtati tu kružnicu, ali moguće je misliti o kružnici koja je zakrivljena prema vani.[ako bi je nacrtali izgledala bi kao obična kružnica, jedino bi trebalo imati na umu da su „vani“ i „unutra“ zamijenili mjesta] Kod obične kružnice zakrivljenost je prema unutra, zar ne? Ako liniju pratimo okolo ona se vraća u sebe. Ali definirajući kružnicu na ovaj drugi način, ako koristimo nužnu konstantu, dobijemo ravnu liniju. Zakrivljenost je još na ovoj strani (desno od osi y). Ali sada stvari čini ni blizu tako ugodnima kao ranije! Ranije, zakrivljenost je uvijek okrenuta prema središtu kružnice, dok nam je sada (u slučaju ravne linije), pokazano da je središte negdje na beskonačnoj udaljenosti, kako se kaže. Idući dalje od ovoga, za nas je javlja ideja o kružnici koja je zakrivljena prema vani. Njena zakrivljenost nije više kao ovdje (Slika 9a) — to bi bila obična, otrcana, filistarska kružnica, — već je njena zakrivljenost ovdje (Slika 9b). Dakle, unutrašnjost ove kružnice nije ovdje; ovo je izvana; unutrašnjost ove kružnice (Slika 9c) je na desno.

Slika 9
Sada usporedite ono što sam upravo stavio pred vas. Opisao sam krivulju Cassini, u njenim raznim oblicima, lemniskate i u obliku u kojem postoje dva ogranka. I sada smo na takav način predstavili kružnicu da je u jednom trenutku zakrivljena na poznati način, s iznutra ovdje i izvana ovdje; dok kod drugog oblika kružnice (crtajući ga samo pokazujemo ono na što se misli) nalazimo da je zakrivljenost ovako obrnuta, s unutra ovdje a izvana ovdje. Uspoređujući je s krivuljom Cassini, prvi oblik kružnice bi odgovarao zatvorenim oblicima, sve do lemniskate. Nakon toga imamo drugu vrstu kružnice, koja mora biti promišljana u drugom smjeru, zakrivljena na ovaj način, s unutra ovdje a izvana ovdje. Vidite, kada nas zanima konstantni umnožak nalazimo oblike krivulje Cassini gdje smo, točno je, bačeni izvan prostora, ipak još uvijek možemo nacrtati drugi ogranak na drugoj strani. Drugi ogranak je opet u prostoru, premda smo pri prijelazu od jednog do drugog izbačeni iz prostora. Ovdje, u slučaju kružnice, međutim, stvar postaje još teža. Pri tranziciji od kružnice do ravne linije mi smo, zaista, izbačeni iz prostora, i štoviše, ne možemo više uopće nacrtati samostalan oblik. To nismo u stanju. Prelazeći od krivulje konstantnog umnoška na krivulju konstantnog kvocijenta, prostorno možemo samo ukazati na misao.
Iznimno je važno da se bavimo kreiranjem ideja koje će, takoreći, skliznuti u ovakve oblike krivulja. Uvjeren sam sa većina ljudi koji se bave matematikom opažaju ovakve diskontinuitete, ali misao čine udobnijom jednostavno držeći se formule i ne prenose ono što matematičkoj formuli treba pridružiti u pravom kontinuitetu misli. Također nikada nisam vidio da je u tretiranju matematike kao teme za obrazovanje ikakva vrijednost dana formiranju ovakvih misli u imaginaciji. — Ne znam, — pitajte prisutne matematičare, g. Blümela, g.Baravallea, da li je to tako; da li je u modernom sveučilišnom obrazovanju tome pridavana ikakva važnost? (Dr. Unger je ovdje spomenuo korištenje filmova.) Da, ali to je izlika. Ovakve stvari unutar empirijskog prostora je pomoću filma ili na sličan način moguće prikazati, samo ako je unesena nekakva obmana. Ne može se potpuno predstaviti u stvarnom prostoru bez da se učinak postigne kroz neki oblik obmane. Poanta je, postoji li išta bilo gdje u sferi stvarnosti nešto što nas obvezuje da mislimo realistički u pogledu ovakvih krivulja. To je pitanje koje sada pitam. Međutim, prije nego idemo dalje, ono što bi možda moglo odgovarati ovim stvarima u oblasti stvarnosti, želio bih dodati nešto što će vam možda olakšati da prijeđete od ovih apstraktnih ideja u stvarnosti. To je slijedeće.

Slika 10
Možete postaviti još jedan problem u sferi teoretske astronomije, teoretske fizike. Možete reći: pretpostavimo da je ovdje kao A, izvor svjetla, i ovaj izvor svjetla osvjetljava točku M (Slika 10). Jačina svjetla koja sjaji od M promatra se od B. Odnosno, s neophodnim optičkim instrumentima, sa B se promatra jačina svjetla koje sija od točke M, koja je osvijetljena od A. I naravno, jačina svijetla bi varirala, u skladu s udaljenosti između B i M. Međutim postoji staza koju točka M može opisati, tako da, osvijetljena od A, uvijek natrag na B sija s jednakim intenzitetom. Postoji takva staza; i stoga možemo pitati: što mora biti geometrijsko mjesto točke, osvijetljene iz fiksne točke A, tako da je, gledano s druge fiksne točke B, njeno svjetlo uvijek istog intenziteta? Ta krivulja — krivulja po kojoj bi se takva točka morala kretati — krivulja je Cassini! Iz ovoga vidite da je nešto što poprima kvalitativnu prirodu postavljeno u prostorne odnose, uklapajući se u složenu krivulju. Kvaliteta koju moramo vidjeti u zraci svjetla — jer intenzitet svjetla je kvaliteta — u ovom slučaju zavisi o elementu oblika u prostornim odnosima.
Ovo sam želio iznijeti za vas samo da vidite da postoji barem neki način prelaska od onog što se može shvatiti u geometrijskom obliku do onog što je kvalitativno. Taj put je dugačak, i ono što ćemo sada raspravljati nešto je na što vam želim skrenuti pažnju, premda će trebati mjeseci za pokazati sve detalje. Morate biti potpuno svjesni da vam namjeravam dati samo linije vodilje; na vama je da ih razvijete dalje i idete u sve detalje koji će potvrditi istinu onog što je rečeno. Jer vidite, veza koju treba uspostaviti između duhovne znanosti i današnje empirijske znanosti zahtijeva veoma dalekosežan i opsežan rad. Međutim kada su dane smjernice, taj rad se u određenoj mjeri može poduzeti i provesti. To je u svakom slučaju moguće. Treba samo moći na konkretan način prodrijeti u empirijske pojave.
Ako se sada latimo problema iz sasvim drugog ugla, — nastojali smo ga u određenoj mjeri razumjeti s matematičkog aspekta, tada, za svakog tko proučava čovjekov organizam, postoji nešto što ne može biti neprimijećeno, nešto što se često iznosilo u našem krugu, posebno u razgovorima koji su pratili ciklus predavanja o medicini u Dornachu, u proljeće 1920. Ne smije se previdjeti da postoji izvjesna veza između organizacije glave i ostatka čovjekove organizacije, na primjer metabolizma. Zaista postoji veza, u početku neodređena, između onog što se odvija u trećem sustavu ljudskog bića — u svim organima metabolizma — i onog što se odvija u glavi. Odnos je tu, ali ga je teško formulirati. Jasno je da se pojavljuje u raznim pojavama, — na primjer, očigledno je da su određene bolesti povezane s lubanjom ili deformacijama glave i slično, i tim stvarima je lako ući u trag s biološkim rezoniranjem, — ipak je teško taj odnos dokučiti u imaginaciji. Ljudi obično ne idu dalje od točke da kažu da mora postojati neka vrsta povezanosti između onog što se odvija u glavi, na primjer, i u ostatku čovjekova organizma. To je slika koju je teško formirati, upravo zato jer je ljudima toliko teško napraviti tranziciju od kvantitativnog aspekta do kvalitativnog. Ako preko duhovno znanstvene metode nismo obrazovani da pronađemo tu tranziciju, sasvim nezavisno od onog što nudi vanjsko iskustvo — proširiti ono što je kvalitativno vrstom misli koju koristimo za kvantitativno, ako se metodički ne izvježbamo da to napravimo, onda će, moji dragi prijatelji, uvijek postojati očita granica našem razumijevanju vanjskih pojava.
Dopustite da ukažem na samo jedan način na koji se možete izvježbati metodološki da kvalitativno promišljate na sličan način kao i kvantitativno. Svi ste upoznati s fenomenom solarnog spektra, običnog kontinuiranog spektra. Znate da tamo imamo tranziciju boje od crvene do ljubičaste. Znate, također, da se Goethe hrvao s problemom kako je taj spektar na neki način obrnut od onog što se mora pojaviti ako se pusti da tama prođe kroz prizmu na isti način na koji se to obično radi sa svjetlom. Rezultat je vrsta okrenutog spektra, i kao što znate Goethe je upriličio i taj pokus također. Kod običnog spektra, zelena prelazi na jednu stranu prema ljubičastoj i na drugu prema crvenoj; dok kod spektra dobivenog od Goethea primjenjujući na prizmu prugu tame postoji boja breskvinog cvijeta u sredini i zatim opet na jednoj strani crvena a na drugoj ljubičasta (Slika 11). Dobivena su dva pojasa boje, središta kojih su nasuprot jedno drugom, kvalitativno nasuprot, i izgleda da se oba pojasa šire takoreći u beskonačnost. Ali sada, može se zamisliti da ova os, longitudinalna os običnog spektra, nije jednostavno ravna linija, već kružnica, kao što je zaista svaka ravna linija kružnica. Ako je ova ravna linija kružnica, vraća se u sebe, i točku gdje se javlja boja breskvina cvijeta možemo smatrati za istu točku kao i onu u kojoj se ljubičasta, šireći se desno, susreće s crvenom, koja se proteže lijevo. Susreću se na beskonačnoj udaljenosti na desno i lijevo. Ako ćemo uspjeti — možda znate da će jedan od prvih pokusa u našem novo osnovanom fizikalnom laboratoriju biti u tom smjeru — ako ćemo uspjeti u savijanju spektra u sebe na određeni način, tada će čak i oni koji nisu u početku skloni stvar shvatiti u čistoj misli, moći vidjeti da se mi ovdje bavimo s nečim stvarnim i kvalitativne prirode.
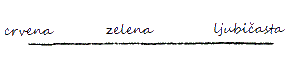
Slika 11
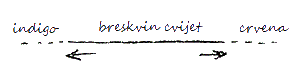
Slika 12
Dolazimo do određenih ograničavajućih ideja u matematici, gdje smo — kao u sintetičkoj geometriji — ravnu liniju dužni gledati kao kružnicu u sasvim realnom premda unutarnjem smislu; gdje smo dužni priznati za beskonačno udaljenu točku ravne linije da je samo jedna točka; ili shvatiti da ravninu ograničava, ne neka linija iznad i zatim opet ispod, već jedna ravna linija; ili promišljati granicu beskonačnog prostora, ne u prirodi nečeg sferičnog, već kao ravninu. Ovakve ideje, međutim, također postaju, na neki način, ograničavajuće ideje za čulima opazivu empirijsku stvarnost, ako se želimo ograničiti samo na čulnu empirijsku stvarnost.
Ovo nas dovodi do nečeg što bi inače uvijek stalno ostalo u mraku. To sam već spomenuo. To nas zaista poziva da promislimo do čega dolazimo kada pustimo da krivulja Cassini oblika lemniskate prijeđe u oblik s dva ogranka, — oblik s dva ogranka za koji moramo ići izvan prostora, — i zatim to usporedimo s onim s čime smo suočeni u empirijskoj stvarnosti.
Vi to zaista već radite, moji dragi prijatelji, kada matematiku na ovaj ili onaj način primijenite na empirijsku stvarnost. Vi trokut zovete trokutom, jer ste ga najprije konstruirali matematički. Na vanjsku formu primjenjujete ono što je razvijeno na unutarnji konstruktivan način u vama. Proces koji sam upravo opisao samo je složeniji, ali to je isti proces kao kada mislite o dva ogranka tog konkretnog oblika krivulje Cassini kao o jednom. Ovu misao primijenite na vezu između čovjekove glave i ostatka čovjekova organizma i morati ćete shvatiti da u glavi postoji veza s ostatkom organizma upravo takvog karaktera kao što je izraženo jednadžbom koja zahtijeva, ne kontinuiranu krivulju, već diskontinuiranu. To se ne može pratiti anatomski; morate ići izvan onog što tijelo uključuje fizički, ako ćete pronaći vezu između onog što nalazi izraz u glavi s onim što nalazi izraz u metaboličkom sustavu. Esencijalno je ljudskom organizmu pristupiti s mislima koje su sasvim nedostižne ako za svaki element vaše misli inzistirate na potpunom podudaranju s čulno opazivom empirijskom oblasti. Moramo dohvatiti nešto drugo, izvan čulno opazive empirijske oblasti, ako ćemo naći što taj odnos stvarno jest unutar ljudskog bića.
Ovakvo proučavanje, ako mu se stvarno preda i provedeno je metodički, iznimno je bogato rezultatima. Čovjekova organizacija je takve prirode da ne može biti obuhvaćena samo anatomskim pristupom. Baš kao što smo kod Cassini krivulje istjerani iz prostora, tako smo i kod proučavanja čovjeka istjerani iz tijela, od same metode proučavanja. Vidite, sasvim je moguće razumjeti u prvom redu u mislima, da smo kod proučavanja cijelog čovjeka izbačeni iz oblasti onog što se može dokučiti u fizičko-empirijskom smislu. Iznijeti ovakve stvari nije napad na znanstvene principe. Ovakve ideje su daleko od čisto hipotetičkih fantazija koje se često uvode u vezi s prirodnim pojavama, jer one se odnose na cjelokupan način na koji je čovjek pripadnik univerzuma. Vi ne tražite nešto što inače ne postoji, već radije nešto što je potpuno isto kao i ono što je izraženo u odnosu između čovjeka koji misli matematički i empirijske stvarnosti.
To nije pitanje traženja hipoteza koje u konačnici nisu opravdane; to je pitanje, pošto je stvarnost očito složena, traženja drugih kognitivnih odnosa s unutarnjom stvarnošću, kao dodatak jednostavnom odnosu matematičkog čovjeka prema empirijskoj stvarnosti. Kada ste jednom prihvatili ovakve misli, također ćete biti navedeni da pitate da li ono što se odvija izvan ljudskog bića u drugim oblastima osim astronomske, — na primjer, kod onih pojava koje zovemo kemijske i fizikalne, — da li te iste pojave, koje gledamo kao kemijske pojave izvan čovjeka, uzimaju isti kurs unutar čovjeka, kada je on živ, kao što to rade izvan njega, ili da li je i ovdje također, nužna tranzicija koja na neki način vodi izvan prostora.
Sada razmotrite važno pitanje koje se iz ovoga javlja. Recimo da ovdje imamo neku vrstu kemijske pojave a ovdje granicu koja vodi preko unutar ljudskog bića (Slika 13). Pretpostavljajući da je ova kemijska pojava mogla izazvati drugu, tako da je ljudsko biće reagiralo ovdje (unutra); tada, ako ostajemo u polju empirijskog, prostor bi naravno bio posrednik. Ako, međutim, do nastavljanja ove pojave unutar ljudskog bića dolazi zahvaljujući činjenici da je, recimo, hranjeno, i procesi koji se već odvijaju izvan njega nastavljaju se u njemu, tada se javlja pitanje: Da li sila koja je na djelu u kemijskom procesu ostaje u istom prostoru kada se odvija unutar čovjeka kao i kada svoj tijek ima izvan njega? Ili moramo li možda ići izvan prostora?
I tu imate ono što je analogno kružnici koja prelazi u ravnu liniju. Ako tražite njen drugi oblik, gdje je ono što je obično okrenuto prema vani sada okrenuto prema unutra, vi ste u potpunosti izvan prostora.
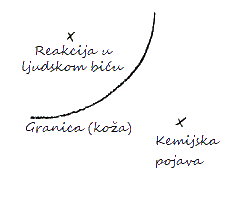
Slika 13
Pitanje je, da li trebamo ideje kao što su te, misaone slike koje, ostajući kontinuirane, idu ravno izvan prostora, — kada slijedimo tijek onog što se događa izvana, izvan čovjeka, u unutrašnjost ljudskog bića. Jedina stvar koja će se reći protiv ovakvih stvari, moji dragi prijatelji, je da one zasigurno nameću veće zahtjeve za ljudsku sposobnost razumijevanja nego ideje s kojima se danas pristupa pojavama. Stoga mogu biti prilično neprijatne u sveučilišnom obrazovanju. One su, bez sumnje, sasvim neprijatne, jer podrazumijevaju da prije pristupanju pojavama moramo u nama probuditi ono što će nam omogućiti da ih razumijemo. Ništa takvog ne postoji u našem obrazovnom sustavu danas; ali treba ući, sigurno mora ući, inače jednostavno govoreći o pojavi dolazimo do najvećeg nepodudaranja, bez da na bilo koji način vidimo stvarnost. Samo promislite što se događa kada netko promatra kružnicu zakrivljenu na ovu stranu (Slika 9a), i zatim vidi kako je zakrivljena na ovu stranu (Slika 9b), ali onda ostaje sitničav i jednostavno ne shvaća da je kružnica sada zakrivljena prema dugoj strani. On kaže: Ovo je nemoguće, kružnica ne može vijugati na ovaj način; krivinu moram staviti ovako okolo, moram jednostavno smjestiti sebe na drugu stranu. Ono što govori izgleda kao jedna te ista stvar; ali on je promijenio njegovo gledište.
Na ovaj način danas stvari pravimo jednostavnim, opisujući ono što je unutar ljudskog bića u usporedbi s onim što se odvija u prirodi izvan njega. Kažemo: Ono što je unutar čovjeka to uopće ne postoji; moram se jednostavno smjestiti unutar čovjeka i reći da je zakrivljenost okrenuta ovamo (Slika 9c). Zatim ću razmatrati ono što je unutra, bez da uzmem u obzir da sam preokrenuo zakrivljenost. Unutrašnjost ljudskog bića načiniti ću vanjskom prirodom. Jednostavno zamišljam da se kroz kožu vanjska priroda nastavlja u unutrašnjost. Ja se sam okrećem, jer ne želim priznati drugi oblik zakrivljenosti, i zatim teoretiziram. Taj se trik radi danas, samo da bi se držali udobnijih kretanja. Ne želi se prihvatiti ono što je stvarno; da to ne bismo napravili, mi jednostavno okrećemo sebe, i — ovo je sada usporedba — umjesto da gledamo na ljudski oblik sprijeda, mi otraga gledamo na prirodu i na ovaj način stižemo do raznih teorija koje se tiču čovjeka.
Nastaviti ćemo, dakle, sutra.
 .
.